ド・モルガンの法則
♪♥ この教材は，高校数学の基本問題のうち，ド・モルガンの法則のバックアップおよびマイナーチェンジありのカバー版です．
♫♣ 元の教材が通信トラブルで読めないときや，元の教材がなくなってしまったとき（高齢者がいつまでも生きている訳ではない）などに，こちらを使ってください．なお，学習の記録は付いていません．
【単元の目次】
《数学Ⅰ・Ａ》
• 数と式 • 根号計算 • 場合の数.順列.組合せ • 確率 • ２次関数• ２次不等式 • 集合・命題・条件・証明
※このページは,PC用です．スマホでは画面の右半分が見えていない場合がありますので，注意してください．
== ド・モルガンの法則 ==
■　共通部分，和集合
(1)　２つの集合A , Bの両方に属する要素全体の集合をA , Bの共通部分といいA∩Bで表す．
(2)　２つの集合A , Bの少なくとも一方に属する要素全体の集合をA , Bの和集合といいA∪Bで表す．

(1)　共通部分は集合の要素が満たすべき条件を「かつ」で結んだ場合に対応している．
A∩B = { x | x∈A かつ x∈B }
(2)　和集合は集合の要素が満たすべき条件を「または」で結んだ場合に対応している．
A∪B = { x | x∈A または x∈B }

※　数学で使われる「AまたはB( A or B )」という用語は，上の(2)から分かるようにAだけ，Bだけというようなどちらか一方だけの場合だけでなく，A∩Bの場合も含んでいることに注意
　したがって，Aが朝にコーヒーを飲む人の集合，Bを朝に紅茶を飲む人の集合とするとき，A∪Bには両方とも飲む人も含まれている．
例１
　A = { 1 , 2 } , B = { 2 , 3 }のときA∩Bを要素を書き並べて示しなさい．
（解答）
　A∩B = { 2 }
例２
　A = { 1 , 2 } , B = { 2 , 3 }のときA∪Bを要素を書き並べて示しなさい．
（解答）
　A∪B = { 1 , 2 , 3 }
例３
　右図において(A∩C)∪Bを要素を書き並べて示しなさい．
（解答）
A∩C = { 4 , 3 }
B = { 2 , 3 , 5 , 6 }
だから
(A∩C)∪B = {2, 3, 4, 5, 6}
ド・モルガン（de Morgan）1806年～1871年 イギリスの数学者で確率論や論理学に業績がある
　共通部分や和集合が組み合わされているときは，かっこの中を先に考えて合成する．
(1)　(A∩B)∪Cを図示するには
まず　A∩B　と　C　を考える．
∪
次に，それらの和集合を考える．
⇒　
(2)　A∩(B∪C)を図示するには
まず　A　と　B∪C　を考える．
∩
次に，それらの共通部分を考える．
⇒　
※　上の(1)(2)から分かるように，
　一般に(A∩B)∪CとA∩(B∪C)は異なる集合になるので，式の中に使われている「かっこ」は省略できない．
　これに対して，(A∩B)∩CとA∩(B∩C)は常に同じ集合になり，どちらの意味に理解されても混乱は起こらないのでA∩B∩Cと書くことができる．
　A∪B∪Cも同様
■　補集合
　全体集合Uの要素のうちで集合Aに属さない要素の集合をAの補集合といいA で表す．

　補集合については次の関係が成り立つ．
A∪A=U
A∩A=∅
A=A

　補集合は条件の「否定」（～でない）に対応している．
A = { x | x∉A }
正確に言えば
A = { x | x∈U かつ x∉A }

※　補集合は全体集合を指定しないと決まらない．
　例えば，偶数の集合の補集合が奇数の集合となるのは，全体集合を整数の集合とした場合であって，全体集合を実数の集合としているときは偶数の集合の補集合には奇数の他に約分できない分数や無理数も含まれる．
(1)　A∩B はA∩Bを作ってからその補集合を考えたものを表す．
　⇒　

(2)　A∩B はAの補集合とBの補集合の共通部分を表す．
∩
　⇒　

※　上の(1)(2)から分かるようにA∩BとA∩Bは全く異なるものになる．
【重要】
　”屋根”がつながっているかどうかで全く違うものになる
例４
　右図において次の各集合を要素を書き並べて示しなさい．
(1)　A∩B∩C
(2)　A∩(B∩C)
(3)　A∩(B∪C)
(4)　A∪(B∩C)

（解答）
(1)　A = { 5 , 6 , 7 , 8 } , B = {2 , 3 , 5 , 6} , C = { 3 , 4 , 6 , 7 } だから A∩B∩C = { 6 }
(2)　B∩C = { 3 , 6 }だからB∩C = { 1, 2, 4, 5, 7, 8}
また A = { 1 , 2 , 3 , 4 }
ゆえに A∩(B∩C) = {1, 2, 4}
 (3)　A = { 5 , 6 , 7 , 8 }
また B∪C = { 2 , 3 , 4 , 5 , 6 , 7 }
ゆえに A∩(B∪C) = { 5 , 6 , 7 }
(4)　B∩C = { 3 , 6 }だからB∩C = { 1, 2, 4, 5, 7, 8}
また A = { 1 , 2 , 3 , 4 }
ゆえに A∪(B∩C) = { 1, 2, 3, 4, 5, 7, 8}
■（集合について）　ド・モルガンの法則

A∩B = A∪B …(1)
A∪B = A∩B …(2)
(1)　←：
A∩B
A∩B

　⇒　 …(i)
A
B


A∪B

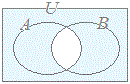　⇒　 …(ii) (i)(ii)は等しい
 (2)　←：
A∪B
A∪B

　⇒　 …(i)
A
B


A∩B

　⇒　 …(ii) (i)(ii)は等しい
例５
　次の各集合のうちで等しいものを選びなさい．
(1)　(A∩B)∩C
(2)　(A∩B)∪C
(3)　(A∪B)∩C
(4)　(A∪B)∩C
 (5)　(A∪B)∩C
(6)　A∩(B∪C)
(7)　(A∩B)∪C
(8)　A∪B∪C
（解答）
(1)→(A∩B)∩C=(A∩B)∪C=(A∪B)∪C→(8)
(2)→(A∩B)∪C=(A∩B)∩C=(A∪B)∩C→(5)
(3)→(A∪B)∩C=(A∪B)∪C=(A∩B)∪C→(7)
(4)→A∪(B∩C)=A∩(B∩C)=A∩(B∪C)→(6)
■　論理についてのド・モルガンの法則
■　（「かつ」「または」について）ド・モルガンの法則
(1)（aかつb）でない=（aでない）または（bでない）
(2)（aまたはb）でない=（aでない）かつ（bでない）
⇒否定にすると「かつ」と「または」が入れ替わる

例６
(1)（x>1かつx≦10）でない
=（x>1でない）または（x≦10でない）
=（x≦1）または（x>10）
 □論理についてのド・モルガンの法則は，集合についてのド・モルガンの法則に対応している．
「かつ」を∧で，「または」を∨で，否定（～でない）を で表すと，論理についてのド・モルガンの法則は次の形に書ける．
a∧b = a∨b
a∨b = a∧b

例７
(2)（x=1またはx≠10）でない
=（x=1でない）かつ（x≠10でない）
=（x≠1）かつ（x=10）
※以下は2010年度現在の高校数学Aの教科書には出ていないが，方程式や不等式の解を考えるときに普通に使われる考え方である．
■（「すべて」「ある」について）ド・モルガンの法則
(1){ すべてのxについてp(x)}でない
=あるxについて{ p(x)でない }
(2){ あるxについてp(x) }でない
=すべてのxについて{ p(x)でない }

⇒否定を作ると「すべて(all)」と「ある(some , exist)」が入れ替わる

（解説）
xが多数あるとき（x1 , x2 , ··· ,xn）
(1)
{ すべてのxについてp(x)}でない
={p(x1 ) かつ p(x2 ) かつ ··· p(xn )}でない
={p(x1 )でない} または {p(x2 )でない} または ··· {p(xn )でない}
となるから
あるxについて{ p(x)でない }
に等しい．
(2)
{ あるxについてp(x)}でない
={p(x1 ) または p(x2 ) または ··· p(xn )}でない
={p(x1 )でない} かつ {p(x2 )でない} かつ ··· {p(xn )でない}
となるから
すべてのxについて{ p(x)でない }
に等しい．
「すべての」を∀，ある（存在する）を∃で表すとき
(1)∀x(p(x))=∃x(p(x))
(2)∃x(p(x))=∀x(p(x)) 		※「すべての」「ある」を意識して解くべき不等式の例
例えば，２次不等式x2−6x+9<0を解きたいとき
この問題は，x2−6x+9<0を満たすxの値の範囲を求めるものであるが，そもそも
「x2−6x+9<0が成り立つxはあるか？」
すなわち
「あるxについてx2−6x+9<0が成り立つか？」…(1)
と考えると，図のように
「すべてのxについてx2−6x+9≧0が成り立つ」…(2)
すなわち，否定(2)が真だから元の命題(1)は偽になる．
したがって，元の問題は「解なし」になる．
例８（この教室にいる学生について）
(1)
（すべての学生は男子である）を否定するには
（ある学生は女子である）ことを示せばよい．（全員女子であることを示す必要はない）
(2)
（男子がいる）を否定するには
（全員女子である）ことを示せばよい．（女子がいることを示すだけでは足りない）

例９（自然数xについて）
元の命題：「すべてのxについて，x>1が成り立つ」
の否定命題は：「あるxについて，x≦1が成り立つ」
（この例では否定命題が正しい［x=1のときがあるから］）
例10（実数xについて）
「あるxについて，2x+1≧0が成り立つ」の否定は
「すべてのxについて，2x+1<0が成り立つ」
（この例では元の命題が正しい［元の不等式に解があるから］） 		例11（自然数m , nについて）
「あるmについて，どんなnをもってきても，m≦nが成り立つ」…(*1)
（このように書かれるときは，mを先に決め，nの値は後から決める．特にnの値はmの値に応じて決めてもよい．
(*1)の命題は真 … この命題は，自然数には最小値m=1が存在するということを表している．）
例12（自然数m , nについて）
例11の否定は
「すべてのmについて，あるnが存在して，m>nが成り立つ」…(*2)
（mを先に決め，nの値は後から決める．特にnの値はmの値に応じて決めてもよい．
(*2)の命題は偽 … m=1のとき，m>nとなるような自然数nは存在しない．）
例13（自然数m , nについて）
「あるmが存在して，どんなnについても，m≧nが成り立つ」…(*3)
（決め方の順序は上記例11，12と同様．nの値は「後だしジャンケン」のようにmの値を聞いてから決めてもよい．
(*3)の命題は偽 … n=m+1とすればn>mとなるから．このことは自然数には最大値が存在しないことを示している．）
■上の例に示したように，∀，∃に対応する日本語としては様々な言い方がある．
∀x：「すべてのxについて」「どんなxについても」「任意のxについて」
∃x：「あるxについて」「xが存在する」「適当なxを選べば」
■「かつ/または」，「すべて/ある」のド・モルガンの法則の組み合わせ
例14（実数xについて）
「あるxについて，（x≧0かつx<3）が成り立つ」
の否定は
「すべてのxについて，（x≧0かつx<3）でない」
＝「すべてのxについて，（x<0またはx≧3）」
［参考］- - - - - （元の命題が正しい：n=1など）
 例15（正の整数nについて）
「すべてのnについて，（nは偶数である，または，3の倍数）」
の否定は
「あるnについて，（nは偶数である，または，3の倍数）でない」
＝「あるnについて，（nは奇数である，かつ，3の倍数でない）」
［参考］- - - - - （否定が正しい：n=1など）
問題１
A = { 2 , 3 , 4 , 6 } , B = { 3 , 5 , 6 }のとき，次の集合を要素を書きならべて示せ．（１つ選べ）
(1)A∩B
{ 1 }___ { 3 }___ { 6 }___ { 3 , 6 }
{ 3 , 4 , 6 }___ { 3 , 5 , 6 }
(2)A∪B
{ 3 }___ { 6 }___ { 2 , 4 }___ { 3 , 6 }
{ 2 , 4 , 5 }___ { 2 , 3 , 4 , 5 , 6 }

問題２
右図において次の集合を要素を書きならべて示せ．（１つ選べ）
(1)(A∪B)∩C
{ 3 }___ { 2 , 3 }___ { 1 , 2 , 5 }___ { 2 , 3 , 4 }
{ 1 , 2 , 3 , 4 }___ { 2 , 3 , 4 , 6 }
(2)(A∪B)∩C
{ 3 }___ { 7 }___ { 8 }___ { 4 , 6 , 7 }
{ 2 , 3 , 4 , 6 }___ { 2 , 3 , 4 , 6 , 7 }
(3)(A∩B)∪C
{ 3 }___ { 8 }___ { 2 , 3 }___ { 1 , 5 , 8 }
{ 2 , 3 , 4 , 6 , 7 }___ { 1 , 2 , 3 , 4 , 6 , 7 }
 問題３A∪(B∩C)に等しいものを選べ．
A∪B∪C
A∩B∩C
A∪(B∩C)
A∩(B∪C)

問題４「すべてのxについて，（x≠0またはx≧1）」の否定を次のうちから選べ．
あるxについて(x=0 かつ x<1)
あるxについて(x=0 または x<1)
すべてのxについて（x≠0かつx≧1）
すべてのxについて（x≠0またはx≧1）

問題５m, nを自然数とするとき，「任意のmについて，適当なnを選べば，m≦nが成り立つ」の否定を次のうちから選べ．

任意のmについて，適当なnを選べば，m>nが成り立つ
あるmについて，適当なnを選べば，m≦nが成り立つ
適当なmを選べば，どんなnについても，m≦nが成り立つ
適当なmを選べば，どんなnについても，m>nが成り立つ

コメント

コメントを投稿