|
♪♥ この教材は,高校数学の基本問題のうち,集合と条件,必要条件,十分条件,センター試験問題のバックアップおよびマイナーチェンジありのカバー版です. ♫♣ 元の教材が通信トラブルで読めないときや,元の教材がなくなってしまったとき(高齢者がいつまでも生きている訳ではない)などに,こちらを使ってください.なお,学習の記録は付いていません.
※このページは,PC用です.スマホでは画面の右半分が見えていない場合がありますので,注意してください.
|
|
以下の問題について,カキクケコなどのカタカナが書き込まれた欄に「半角数字(1バイト文字の数字)」を入力してください.
(初めに見えているカナは,マウスでポイントすれば消えますので,その場所に数字を書き込んでください) |
(やさしい:2つの条件の間に
 を書き,成立する方の矢印で「十→要」を判断するとよい。 を書き,成立する方の矢印で「十→要」を判断するとよい。○ m+n は 2 で割り切れる  m は 2 で割り切れ,かつ n は 4 で割り切れる m は 2 で割り切れ,かつ n は 4 で割り切れる〇→ m+n が 2 で割り切れても,m=1 , m=3 のとき,「m は 2 で割り切れ,かつ n は 4 で割り切れる」とは言えないから,→は× 〇← 「m=2k かつ n=4l (k,l は整数)」ならば m+n=2(k+2l) は,2 で割り切れるから,←は○ 〇答 p  rだから「pはrであるための必要条件」:1
○ 上記の対偶を考えると
p rだから「pはrであるための必要条件」:1
○ 上記の対偶を考えると
p  r だから 「p は r であるための十分条件」:2
○ m+n=2k かつ n=4l(k,l は整数) r だから 「p は r であるための十分条件」:2
○ m+n=2k かつ n=4l(k,l は整数) m=2s かつ n=4t(s,t は整数) m=2s かつ n=4t(s,t は整数)
〇→ m+n=2k かつ n=4l(k,l は整数)ならば,「m=2k−4l=2(k−2l) は 2 で割り切れ,かつ n=4l」だから,→は○ 〇← 「m=2k かつ n=4l (k,l は整数)」ならば m+n=2(k+2l) は,2 で割り切れるから,←は○ 〇答 「p かつ q」  r だから 「p かつ q」 は r であるための必要十分条件」:0
○ m+n=2k または n=4l(k,l は整数) r だから 「p かつ q」 は r であるための必要十分条件」:0
○ m+n=2k または n=4l(k,l は整数) m=2s かつ n=4t(s,t は整数)
→? m=2s かつ n=4t(s,t は整数)
→?m=n=1 のとき,m+n=2k または n=4l が成り立つが,m=2s かつ n=4t とはいえないから,→は× ←? 「m=2s かつ n=4t 」ならば n=4t だから,←は○ 「p または q」p  r だから 「p かつ q」 は r であるための必要条件」:1 r だから 「p かつ q」 は r であるための必要条件」:1
|
|
(2つの条件の間に  を書き,成立する方の矢印で「十→要」を判断する。または,集合 P⊂Q のとき,条件 p→q とする。 を書き,成立する方の矢印で「十→要」を判断する。または,集合 P⊂Q のとき,条件 p→q とする。(1) 2で割り切れるものの集合を P とおくと, A={10 ,20, 30, ... } P={2 ,4, 6, 8, 10, 12, ... , 20} だから A⊂P(十分条件:2)
(別解)x∈A → x=10k(k は整数)→ x=2(5k) は2で割り切れるが,逆に x が2で割り切れても,x=6 のように10で割り切れないものもあるから,x∈A
20で割り切れるものの集合を Q とおくと, x∈P (十分条件:2) x∈P (十分条件:2)
B={4 ,8, 12, 16, 20, 24, ...,40, ...} Q={20, 40 , 60, ... , } だから Q⊂B(必要条件:1)
(別解)x∈Q → x=20k(k は整数)→ x=4(5k) は4で割り切れるが,逆に x が4で割り切れても,x=8 のように20で割り切れないものもあるから, x∈B
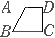
(2) 右図のようになるから x∈Q (必要条件:1) x∈Q (必要条件:1)
C=A∩B→4 D=A∪B→3 E=A∩B→7 |
|
(1) 「かつ」「または」に関するド・モルガンの法則 a かつ b=aまたはb により, a , b はともに有理数 = a は有理数またはb は有理数 =a は無理数 または b は無理数 … 3 (2) 「q かつ r」  p の成否を調べる。 p の成否を調べる。〇←は明らかに成立する。
(a= , b= , m,n,s,t∈Q,Q は有理数全体の集合,b≠0 のとき,
〇→の成否を調べる:a+b=+=∈Q , ab=∈Q , =∈Q だから p⇒「q かつ r」が成立する. ) a , b が有理数でないときでも,次のような場合には a+b , ab , は有理数となる。 a= , b= − のとき a+b=0 , ab=−2 ,=−1 したがって,「q かつ r」⇒p は成立しない.… 1 (3) 「p  q」 q」〇→〇は明らか。 〇←×の反例 a+b=0 , ab=−2 のとき,a=−, b=(またはa=, b=−は有理数でない。 もとの命題「p⇒q」は真,その逆は偽。次に,もとの命題とその対偶とは真偽が一致するから,対偶は真… 2 |
|
(1) |x|=2⇔x=±2…(A) x2−4x+4=0⇔x=2 …(B) x=±2…(A)  x=2 …(B) x=2 …(B)したがって,(A)は(B)の必要条件 … 2 (2) f(x)=x2−ax−b とおくと,f(0)=−b で x2 の係数が正だから b>0⇔f(0)<0⇔  ⇔f(x)=0が正負の実数解をもつ。 したがって,必要十分条件 … 1 (3) a>2 , b>2 の表わす領域は右図黄色の部分 …(A) ab>a+b⇔ab−a−b>0 ⇔(a−1)(b−1)>1の表わす領域は右図灰色の部分 …(B) (A)  (B) したがって,十分条件 … 3 (B) したがって,十分条件 … 3
(別解)
(4)ab>a+b⇔ab−a−b>0⇔(a−1)(b−1)>1 …(A) だから,この式の形に合わせることを考える。 a>2 , b>2 ⇔ a−1>1 , b−1>1 …(B) a−1>1 , b−1>1  (a−1)(b−1)>1を調べる (a−1)(b−1)>1を調べる明らかに, (B)〇→○(A) (B)〇←?(A) は,積が1よりも大きければ両方とも1よりも大きいか?という問題で,両方とも負の数のとき,例えば a−1=−2 , b−1=−3 すなわち a=−1 , b=−2 のとき,(a−1)(b−1)=6>1 であるが a−1=−2<1 , b−1=−3<1 となって成立しない。 (A)  (B) したがって,十分条件 … 3 (B) したがって,十分条件 … 3
P(x)=x2Q(x) → {P(x)}2=x4{Q(x)}2=x3[x{Q(x)}2] だから,〇→○ 〇←? を対偶によって示す。 P(x)=x2Q(x)+ax+b (a , b≠0 ) → {P(x)}2=x4{Q(x)}2+a2x2+b2+2ax3Q(x)+2abx+2bx2Q(x) の1次,2次の項は0にならない。したがって,〇←〇 必要十分条件 … 1 (5) sinA=sinBかつsinC=sinD⇔(B=A または B=180°−A) かつ (D=CまたはC=180°−C)
 sinA=sinB, sinC=sinD となるから sinA=sinB, sinC=sinD となるから必要条件 … 2 |
|
(1) x2=y2⇔(x−y)(x+y)=0⇔x=±y …(A) x3=y3⇔(x−y)(x2 + xy+y2)=0⇔x=y または x2 + xy+y2=0⇔x=y または (x + )2+ y2=0⇔x=y または x=y=0(x=y=0 は x=y に含まれるから )⇔x=y …(B) x=±y  x=yだから,(A)は(B)の必要条件 … 2
(2) x=yだから,(A)は(B)の必要条件 … 2
(2)2x2−4x+1<0⇔0.3≒ <x<≒1.7 …(A) 右のグラフから (x−3)(x−2)(x+2)>0⇔−2<x<2 , 3<x …(B) (A)  (B)だから,(A)は(B)の十分条件 … 3
(3)(危険な落とし穴に注意) (B)だから,(A)は(B)の十分条件 … 3
(3)(危険な落とし穴に注意)鋭角三角形⇔cosA>0 , cosB>0 , cosC>0 …(A) cosA cosB cosC>0⇔cosA>0 , cosB>0 , cosC>0またはcosA , cosB , cosCのうち2つが負,1つが正 ところが,三角形の内角で2つが90°より大きいことはないから,「cosA , cosB , cosCのうち2つが負」ということはない。 したがって,cosA cosB cosC>0 ⇔cosA>0 , cosB>0 , cosC>0 …(B) ゆえに,(A)⇔(B),(A)は(B)の必要十分条件 … 1 (4)(危険な落とし穴に注意。m , n は自然数とされているから,無理数や虚数の場合を考えなくてよい。) 〇→? m=5k , n=5l(m , n は自然数)→m+n=5(k+l) , mn=5(5kl) だから〇→○ 〇←? m+n=5p , mn=5q(p , q は自然数)→mn=5qより m , n の少なくとも1つは5の倍数。対称式だから,m が5の倍数(5r)としても一般性を失わない。このとき,m+n=5pより n=5p−5r=5(p−r)も5の倍数。 したがって,〇←○必要十分条件 … 1 |
|
(1) A∪B=A⇔  ⇔A∩B=B ⇔A∩B=Bだから,必要十分条件 … 1 (2)(2,3の例で調べてみると分かる。) 〇←○ n=12k⇒n2=12(12k2)は明らか。 〇→? n2 が 12 の倍数で,かつ, n が 12 の倍数でないものはないかどうか調べると, n=2·3=6 , 2·32=18 のとき,n は 12 の倍数でないが n2=22·32=12k ,22·34=12l となるから,〇→× したがって,必要条件 … 2 (3)(中学,高校の授業でこれ自体を扱う時間はほとんどないが,証明できるかどうか調べてみると分かる。) △ABCの内接円の中心をIとおくと,次の関係が成り立つ。 △BPI≡△BQI △ABCの外接円の中心をOとおくと,次の関係が成り立つ。 △BMO≡△CMO 正三角形 → 内接円の中心と外接円の中心は一致する。 逆に,内接円の中心と外接円の中心が一致すれば,BP=BQ=CQが成り立ち,同様にしてCQ=CR=AR=APも成り立つからAB=BC=CAとなり,正三角形となる。必要十分条件 … 1 (4)|a+b|≦|a|+|b|(等号は a,b が同符号または0のとき) すなわち,|a+b|=|a|+|b|⇔ab≧0 を公式とすれば |(a+b)+c|=|a+b|+|c|⇔(a+b)c≧0 さらに, |(a+b)+c|=|a+b|+|c|=|a|+|b|+|c|⇔(a+b)c≧0 , ab≧0 したがって, (a+b)c≧0 , ab≧0  (a+b)c+ab≧0 の成否を調べればよい。 (a+b)c+ab≧0 の成否を調べればよい。〇→○ は明らか 〇←? は,和が0以上ならば2つとも0以上と言えるか?ということで 大小アンバランスな例を考えると成立しないことが示せる。 反例:a=6,b=−1,c=8 のとき,(a+b)c+ab=34≧0 であるが,ab=−6<0 したがって,〇←×十分条件 … 3 |









コメント